Many people see math as something that has to do with crunching numbers and maybe working with an x or a y if you’re feeling fresh. However, true pure mathematics relies much more on proving things from the ground up and requires logical thinking and more writing skills than you would think. This being said, I would like to show off some of my favorite math theorems and equations because some of them are just downright beautiful.
The Fundamental Theorem of Arithmetic
The fundamental theorem of arithmetic states that every integer greater than 1 can be expressed uniquely as a product of prime numbers. This one should just get your brain folds massaged and soft at how GORGEOUS it is. EXAMPLE!!!! A number I LOVEEE is 2400. You can write 2400 as (2^5)(3^1)(5^2) which are all prime numbers. Pretty crazy stuff, I know.
The Fundamental Theorem of Calculus
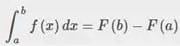
We call F(x) the antiderivative of f(x). This theorem is just amazing for many, many reasons. When you first learn this theorem, it will usually be after units of tediously calculating derivatives and trying to wrap your head around what they really are, so when you find out they have this beautiful application where the AREA under a curve is related to the instantaneous rate of change of the function, it’s a pretty amazing moment. Sometimes when I tell people who don’t know calculus about this result, I feel like I’m spoiling a crazy plot twist that happens in a show; after all, calculus is the epidemy of a drama series.
|ℝ|>|ℕ| (The cardinality of the set of Real numbers is larger than the cardinality of the set of Natural numbers)
This one just had my brain and knees weak when I learned it. It’s basically saying that the size of the real numbers is greater than the size of the natural numbers. This just seems like an insane result because both of these sets of numbers are INFINITE. How can they have different sizes if they’re infinite??!!? Essentially, using deduction and a VERY elegant proof that is too large to fit in this blog, you can show that the infinite cardinality of the real numbers is greater than the infinite cardinality of the natural numbers, and there is no bijection between them.
Schrödinger’s Equation
Look, I know that this isn’t technically a math equation and is definitely classified as physics, but this thing is just so dang gorgeous. I don’t even understand what’s going on yet, but apparently it is used to describe probabilities of electrons which sounds cool. I’m more looking at the absolute sleek and sexy symbols that are used to craft this absolute beauty of an equation. Take a gander everyone.
iħ ∂ψ/∂t = (-ħ²/2m) ∂²ψ/∂x² + V(x)ψ.
Maxwell’s Equations
Guys, I know I’m really starting to sound like a physicist and all, but these equations walk into a room and pants drop. The first time I saw them I think I was watching a YouTube video on the most famous physics equations and I just knew that I was in love. First off, let me tell you that I absolutely love learning about energy and power grids and things of that sort, so seeing these gorgeous equations that describe how some of that works just made me over the moon. Just look at them (P.S. I have to paste them in because there are so many of them).
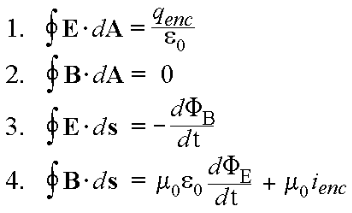
All of these equations and theorems hold a very special place in my heart and they are all ranked evenly, with many more that I love even more that would be too long to put in this blog. I LOVE MATH!!!!

